Площадь треугольника

Содержание:

Треугольник — это геометрическая фигура, состоящая из трех точек, расположенных на одной прямой, и трех отрезков, соединяющих эти точки. Отрезки называются сторонами, а точки — вершинами. Треугольники различаются по величине углов:.

Треугольники также различают по длине сторон.

Равносторонние – три равных стороны.
Равнобедренные – две равных стороны.
Разносторонние ‒ три стороны с разной длиной.

Площадь каждой фигуры рассчитывается несколькими способами: через две или три стороны, тип зеолонга, основание и высоту. Как только вы ее поймете, геометрия сопровождает старшеклассников до окончания школы, а затем и университета, так что в дальнейшем она не вызывает трудностей.

Сегодня существуют онлайн-калькуляторы, которые могут производить расчеты, но прежде чем пользоваться такими помощниками, необходимо разобраться в символах и типах. Без базовых знаний невозможно правильно выполнить расчеты.

Формулы для площади треугольника

Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.

Фигура	Рисунок	Формула площади	Обозначения
Произвольный треугольник			a – любая сторона,h_a – , опущенная на эту сторону
		a и b – две любые стороны,С – угол между ними
	.	a, b, c – стороны,p – Формулу называют «Формула Герона»
		a – любая сторона,B, С – прилежащие к ней углы
		a, b, c – стороны,r – радиус ,p –
		a, b, c – стороны,R – радиус
	S = 2R2 sin A sin B sin C	A, B, С – углы,R – радиус
Равносторонний (правильный) треугольник			a – сторона
		h –
		r – радиус
		R – радиус
			a и b –
		a – ,φ – прилежащий острый угол
		a – ,φ – противолежащий острый угол
		c – ,φ – любой из острых углов

Произвольный треугольник
	гдеa – любая сторона,h_a – , опущенная на эту сторону
	гдеa и b – две любые стороны,С – угол между ними
	. гдеa, b, c – стороны,p – Формулу называют «Формула Герона»
	гдеa – любая сторона,B, С – прилежащие к ней углы
	гдеa, b, c – стороны,r – радиус ,p –
	гдеa, b, c – стороны,R – радиус
	S = 2R2 sin A sin B sin C гдеA, B, С – углы,R – радиус
Равносторонний (правильный) треугольник
	гдеa – сторона
	гдеh –
	гдеr – радиус
	гдеR – радиус

	гдеa и b –
	гдеa – ,φ – прилежащий острый угол
	гдеa – ,φ – противолежащий острый угол
	гдеc – ,φ – любой из острых углов

Произвольный треугольник

гдеa – любая сторона,h_a – , опущенная на эту сторону

гдеa и b – две любые стороны,С – угол между ними

гдеa, b, c – стороны,p –

Формулу называют «Формула Герона»

гдеa – любая сторона,B, С – прилежащие к ней углы

гдеa, b, c – стороны,r – радиус ,p –

гдеa, b, c – стороны,R – радиус

S = 2R2 sin A sin B sin C

гдеA, B, С – углы,R – радиус

Равносторонний (правильный) треугольник

гдеa – сторона

гдеh –

гдеr – радиус

гдеR – радиус

гдеa и b –

гдеa – ,φ – прилежащий острый угол

гдеa – ,φ – противолежащий острый угол

гдеc – ,φ – любой из острых углов

Как найти площадь треугольника по трем сторонам

Представлено множество вариантов для расчёта длины сторон радиуса и площади треугольника. Одна из удобных формул для расчёта площади по трём сторонам называется формулой Герона и используется в том случае, если известна длина всех трех сторон.

Полупериметром называют сумму длин всех сторон разделенную на 2.

Рассмотрим формулу на примере. Нам необходимо найти полупериметр треугольника, где даны следующие стороны a = 5, b = 6, c = 7. Производим расчет:

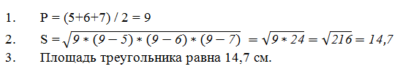
Вычисляя по формуле Герона, вначале мы перемножили полученные результаты, затем из полученного числа извлекли квадратный корень. Конечное значение и является площадью искомого треугольника.

Для полного понимания необходимо постоянно упражняться и заниматься. С каждым разом усложняйте задачу и выбирайте примеры с другими значениями. Систематическое повторение позволит назубок выучить формулу Герона и научиться применять её для решения простых и сложных задач.

Геометрия может пригодиться не только в школе, но и во взрослой жизни, например, тем, кто занимается обустройством интерьера, ремонтами и планирует изучать архитектуру.

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Формула Герона для нахождения площади треугольника:

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Формула нахождения площади треугольника через две стороны и угол между ними:

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Формула нахождения площади прямоугольного треугольника через катеты:

Формула нахождения площади равнобедренного треугольника через две стороны:

Формула нахождения площади равнобедренного треугольника через основание и угол:

Формула нахождения площади равностороннего треугольника через сторону:

Формула нахождения площади равностороннего треугольника через высоту:

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Формулы площади треугольника

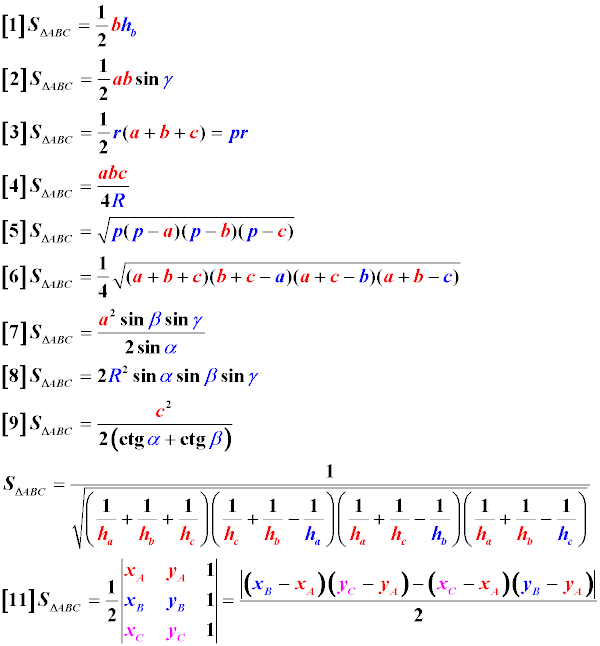
Пояснения к формулам: a, b, c — длины сторон треугольника, площадь которого мы хотим найти r — радиус вписанной в треугольник окружности R — радиус описанной вокруг треугольника окружности h — высота треугольника, опущенная на сторону p — полупериметр треугольника, 1/2 суммы его сторон (периметра) α — угол, противолежащий стороне a треугольника β — угол, противолежащий стороне b треугольника γ — угол, противолежащий стороне c треугольника h_a,h_b_, h_c— высота треугольника, опущенная на сторону a, b, c

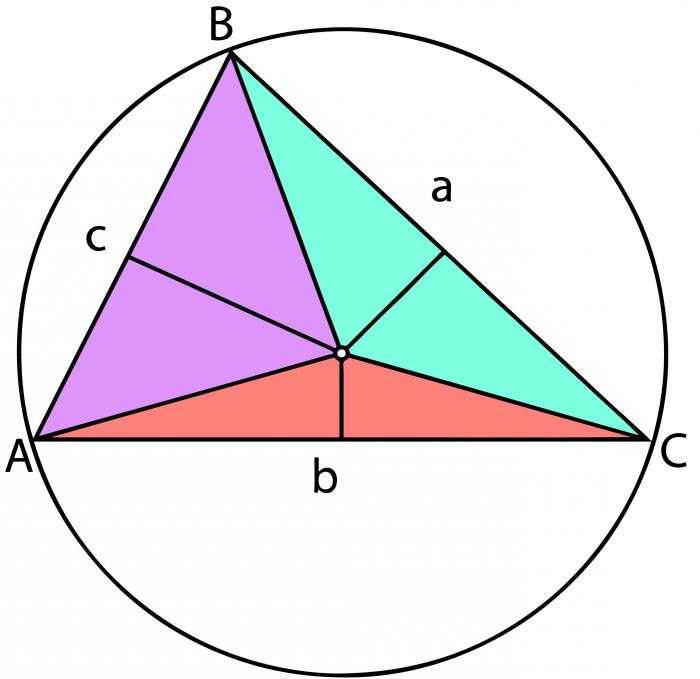
Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.

Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2 ) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)

Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула
Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
Формула 11 позволяет вычислить площадь треугольника по координатам его вершин, которые заданы в виде значений (x;y) для каждой из вершин

Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

См. также площадь равнобедренного треугольника.

Примечание. Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √

Прямоугольный треугольник и его площадь.

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

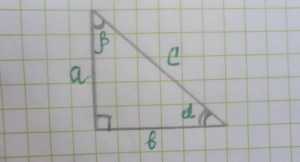
1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:

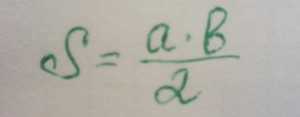
В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.

В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.

2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

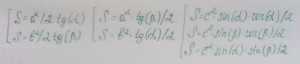
Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Площадь треугольника — калькуляторы для всех видов

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.

Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по основанию и высоте — калькулятор онлайн:

Формула	Результат
S = ½ × a × h
	Сторона a
Высота h

Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по двум сторонам и углу между ними — расчет:

Формула	Результат
S = ½ × a × b × α
	Сторона a
Сторона b
Угол α° между сторонами a и b

Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.

Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:

Формула	Результат
S = r × ½ × (a + b + c)
	Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности

Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:

Формула	Результат
S = (a × b × c) ⁄ (4 × R)
	Сторона a
Сторона b
Сторона c
Радиус R описанной окружности

Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.

Площадь треугольника по формуле Герона — калькулятор онлайн:

Формула	Результат
S = √ p × (p — a) × (p — b) × (p — c)
	Сторона a
Сторона b
Сторона c

Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:

Формула	Результат
S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β))
	Сторона a
Угол β°
Угол α°

Площадь трапеции

Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.

В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:

Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:

Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:

В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:

Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.

Решение. Это простая задача на использование формулы площади трапеции:

Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):

Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:

Считаем площадь:

Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?

Решение. Выполним построение:

Найдем острый угол трапеции. Так как CD||АВ, то

Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:

ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:

Из равенства треуг-ков следует, что

Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.

Свойства треугольника

длина любой стороны треугольника меньше суммы длин двух остальных сторон, но больше разницы длин двух остальных сторон;
высота треугольника образует прямой угол со стороной, к которой проведена;
площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота S_ABC=a⋅h/2.

Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 4 = 7, значит построить треугольник не получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. Так как для укаанных длин будут справедливы следующие равенства: 16 + 18 > 32 и 16 > 32 − 18, то треугольник построить получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 1 см, 3 см, 7 см ?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 1

Пример. Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 4 см, другая сторона, которая образует прямой угол, в 2 раза меньше. Определи площадь треугольника.

Пусть AB = 4 см, тогда сторона BC = 4 : 2 = 2. И тогда площадь треугольника будет равна: S = 2 * 4 : 2 = 4 см2

Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше. Определи площадь треугольника.

Пусть AB = 12 см, тогда сторона BC = 12 : 3 = 4. И тогда площадь треугольника будет равна: S = 12 * 4 : 2 = 24 см2

Рассчитай площадь треугольника ABC, если дана площадь клетки — 1 м2.

В треугольнике от вершины B проведём перпендикуляр к стороне AC. Таким образом данный треугольник разбит на два прямоугольных треугольника. Каждый из них — половина прямоугольника.

Поэтому площадь можно рассчитать следующим образом:

S_ABC=4⋅4/2+3⋅4/2=(16+12)/2=28/2=14м2.

Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.

Известно, что периметр равностороннего треугольника — 21 см.

Значит, одна сторона треугольника равна 7 см.

Периметр данного четырёхугольника состоит из 4 таких сторон, значит, равен 28 см.

Дан равносторонний треугольник. 2 раза сделано следующее:

1. на всех сторонах отмечены и соединены серединные точки. 2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки. Треугольник, который образовался на этот раз, закрашен розовым цветом.

Внутренний треугольник состоит из 4 маленьких треугольников, такими же являются остальные 3 треугольника, следовательно, всего 4⋅4=16 маленьких треугольников.

2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?

Площадь большого треугольника равна 16⋅4=64 м².

3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 4 раза, то общее число маленьких треугольников будет равняться 256.

4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 3 раза, то общее число маленьких треугольников будет равняться 64.

Определи площадь данных фигур, если площадь одной клетки равна 6 см2. 1)

Фигура образует 2 клетки, а ее площадь равна 6 *2 = 12 кв.см.

У второй фигуры будет 8 клеток. Площадь фигуры равна 8 ⋅ 6 = 48см2 .

Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.

У третьей фигуры — 18 клеток, у четвертой — 32 клетки.

Способы нахождения площади

Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.

Через две стороны и угол

Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:

\(S=\frac12a\times b\times\sin\alpha\)

где a и b — стороны фигуры, а α — угол между ними.

Через радиус описанной окружности и три стороны

Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:

\(S=\frac{a\times b\times c}{4\times R}\)

где a, b и c — стороны фигуры, а R — радиус описанной окружности.

Через радиус вписанной окружности и три стороны

В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:

\(S=r\times\frac{a+b+c}2\)

где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.

Таким образом, формулу можно выразить всего двумя множителями:

\(S=r\times p\)

где p — полупериметр треугольника.

Через сторону и два угла

Если в данной фигуры вам известна лишь одна сторона и две прилегающих к ней угла, ее S можно найти следующим образом:

\(S=\frac12\times a^2\times\frac{\sin\alpha\times\sin\beta}{\sin\gamma}\)

причем \(\gamma=180^\circ-(\alpha+\beta)\)

Калькулятор площади для равнобедренных треугольников

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.

Площадь равнобедренного треугольника по боковым сторонам и основанию — калькулятор:

Формула	Результат
S = ¼ × c × √ (4 × a² — c²)
	Сторона a (a = b)
Сторона c

Если известны боковые стороны и угол между ними, то площадь равнобедренного треугольника определяется, как половина произведения квадрата боковой стороны на синус угла между боковыми сторонами.

Площадь равнобедренного треугольника по боковым сторонам и углу между ними:

Формула	Результат
S = ½ × a² × sin (α)
	Боковая сторона a (a = b)
Угол α° между боковыми сторонами

Если известна боковая сторона, основание и углу между ними, то площадь равнобедренного треугольника равна половине произведения боковой стороны и основания на синус угла между ними.

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними — расчет:

Формула	Результат
S = ½ ×a × c × sin (β)
	Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной

Если известно основание и угол между боковыми сторонами, то площадь равнобедренного треугольника рассчитывается, как четверть отношения квадрата основания на тангенс половинного угла между боковыми сторонами.

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами — онлайн:

Формула	Результат
S = c² ⁄ (4 × tg (½ × α))
	Основание треугольника c
Угол α° между боковыми сторонами

Площадь равнобедренного треугольника по высоте и основанию — калькулятор:

Формула	Результат
S = ½ × c × h
	Основание треугольника c
Высота h

Различные типы треугольников в зависимости от длины их сторон

Разносторонний треугольник

Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.

Равнобедренный треугольник

Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.

Прямоугольный треугольник

Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.

Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.

Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.

Равносторонний треугольник

Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

Найти квадрат диагонали (умножить диагональ на саму себя).
Найти половину этого квадрата – умножить его на 0,5.
Найти синус угла между диагоналями.
Умножить половину квадрата диагонали на синус угла между диагоналями.

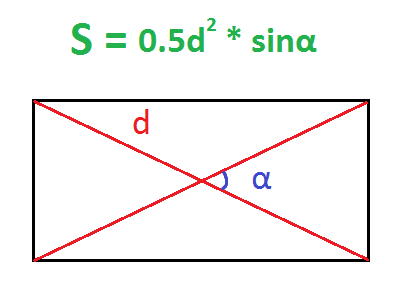
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

Квадрат диагонали: 10*10 = 100 см.
Половина этого квадрата: 0,5*100 = 50 см.
Синус угла между диагоналями: sin 30 градусов = 0,5.
Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

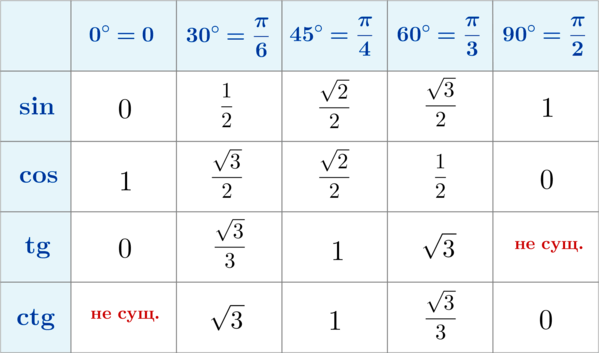
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

Общая формула

4. Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:

S = r * p, где p — полупериметр.

6. Формула Герона для вычисления площади треугольника.

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2

Формулы, которыми можно воспользоваться в разных задачах

Известны длины сторон, и требуется найти площадь равнобедренного треугольника.

В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:

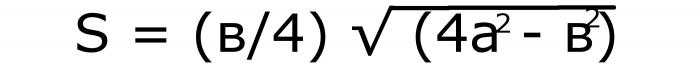
Пусть она будет записана под №1.

Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.

Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:

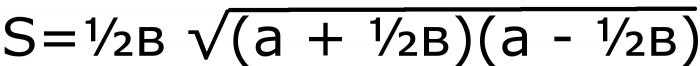
Это формула №2.

Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.

Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:

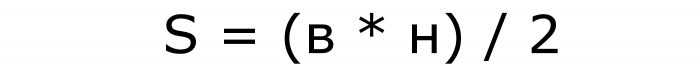
Номер этой формулы — 3.

В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.

Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:

Порядковый номер формулы — 4.

В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.

Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:

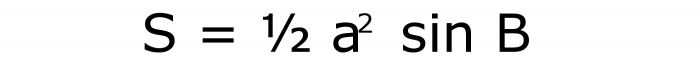
Ее номер — 5.

Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.

Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение. Таким образом, получится такая формула:

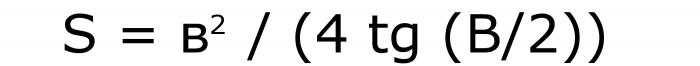
Номер последней формулы — 6.

Способ расчета площади треугольника

Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).Формула площади треугольника: , где a – сторона треугольника, h – высота

Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).Формула площади треугольника: , где a, b – стороны треугольника, α – угол между ними

Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).Формула площади треугольника: , , где r – радиус окружности, p – полусумма сторон

Треугольник – это геометрическая фигура, состоящая из трех точек (вершины треугольника), не лежащих на одной прямой, соедененных тремя отрезками (стороны треугольника).Формула площади треугольника: , где a, b, c – стороны треугольника, R – радиус окружности

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой.Формула площади треугольника: , где a – стороны треугольника

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой.Формула площади треугольника: , где r – радиус окружности

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой.Формула площади треугольника: , где R – радиус окружности

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой.Формула площади треугольника: , где h – высота

Прямоугольный треугольник – это треугольник, в котором один угол прямой (составляет 90 градусов).Формула площади треугольника: , где a, b – катеты

Прямоугольный треугольник – это треугольник, в котором один угол прямой (составляет 90 градусов).Формула площади треугольника: , где d,e – отрезки на гипотенузе

Прямоугольный треугольник – это треугольник, в котором один угол прямой (составляет 90 градусов).Формула площади треугольника: , , где a, b – катеты, p – полусумма сторон

Равнобедренный треугольник – это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя — основанием.Формула площади треугольника: , где a – равные стороны, α – угол между ними

Равнобедренный треугольник – это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя — основанием.Формула площади треугольника: , где b – основание, α – угол между равными сторонами

Площадь разностороннего треугольника

Вычисляем площадь треугольника без особенностей – все его стороны разные и все углы разные.

Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле “площадь треугольника через две стороны и угол между ними”:

Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:

Площадь равнобедренного треугольника

Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.

К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:

Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:

Площадь прямоугольного треугольника

Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:

Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе

Площадь прямоугольного треугольника, если в него вписана окружность:

Площадь равностороннего треугольника

Площадь равностороннего треугольника можно найти через радиус описанной окружности.

Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:

Площадь равностороннего треугольника, если известна сторона треугольника:

Площадь равностороннего треугольника, если известна высота треугольника:

Координаты

При изучении координатных осей задачи, стоящие перед учениками, усложняются. Однако не настолько, чтобы впадать в панику. Для того чтобы найти площадь треугольника по координатам вершин, вы можете воспользоваться всё той же, но немного изменённой формулой Герона. Для координат она приобретает следующий вид:

S=((x₂-x₁)2*(y₂-y₁)2*(z₂-z₁)2)1/2.

Впрочем, никто не запрещает, используя координаты, вычислить длины сторон треугольника и затем, по формулам, которые были написаны выше, посчитать площадь. Для преобразования координат в длину пользуйтесь следующей формулой:

l=((x₂-x₁)2+(y₂-y₁)2)1/2.

Вывод формул для площади равностороннего треугольника

Утверждение 7.

Если a – сторона равностороннего треугольника, то его площадь

Если h – равностороннего треугольника, то его площадь

Если r – радиус , то его площадь

Если R – радиус около равностороннего треугольника окружности, то его площадь

Доказательство.

Рассмотрим рисунок 7.

Рис. 7

В силу утверждения 2

Рассмотрим рисунок 8.

Рис. 8

Поскольку

то

Рассмотрим рисунок 9.

Рис. 9

Поскольку у равностороннего треугольника , то . Следовательно,

Рассмотрим рисунок 10.

Рис. 10

Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство Следовательно,

Доказательство утверждения 7 завершено.