Как найти площадь прямоугольника

Квадратный сантиметр, дециметр, метр

Какой меркой лучше измерить площадь фигуры квадрата и прямоугольника?

В 18 веке на Руси вводилась основная мера измерения площади — десятина и четь. Но поля крестьян были неровными, поэтому часто мерками служила урожайная копна. Народ изобретал особые мерки: выть, соха, обжа, коробь, веревка, жеребья. Сейчас мы не используем этих мер.

Начертите прямоугольник со сторонами 5см и 4см. Какими мерками можно измерить фигуру?

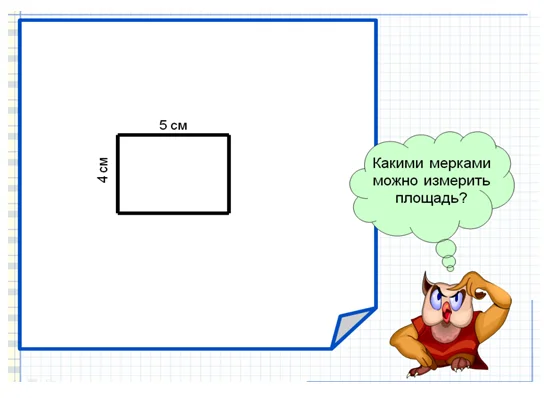
Посмотрите на рисунок, утенок измерил прямоугольник с помощью треугольников, ежонок — квадратами, а котенок — прямоугольниками.

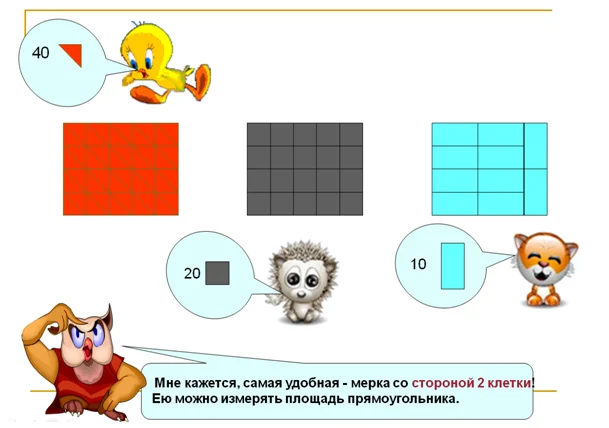
Посчитаем, сколько единичных мерок находится в прямоугольнике. У животных получились разные величины: 40, 20, 10.

Всегда ли удобно определять площадь фигуры произвольными мерками?

Конечно, нет.

Вывод: значение величины зависит от выбранной мерки. Чтобы сравнить, нужно договориться об одинаковом способе измерения.

Всегда ли для определения площади фигуры подходит клетка?

Да.

Какого размера должна быть клетка?

Я предлагаю измерять как ежик, квадратами по 2 клеточки.

Измерьте длину и ширину этого квадратика. Что получилось?

Длина и ширина равна 1 см.

Единицей измерения площади еще 4-5 тысяч лет тому назад жители древнего города Вавилона считали квадрат, так как именно квадрат имеет превосходные признаки: четыре стороны равны межу собой, четыре прямых угла; можно провести ось и найти центр симметрии. Форма квадрата без изъянов, совершенна, поэтому его легко начертить и плотно покрыть фигуры любой формы.

Если у квадратика сторона 1см – площадь его равна квадратному сантиметру.

1 квадратный сантиметр сравним с ноготком взрослого человека.

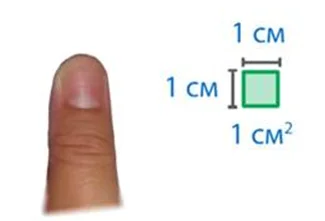
Записывается площадь 1 квадратного сантиметра так:

S = 1 кв. см или S = 1 см2

Латинская буква «эс» обозначает площадь, двойка в правом верхнем углу — две величины: длину и ширину.

Начертите квадрат со стороной 10 сантиметров.

Квадратный дециметр (1 дм 2) — это квадрат со стороной 1 дм или 10 см.

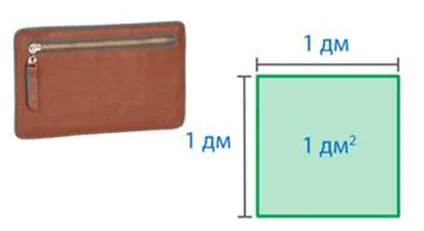
Квадратный метр (1 м 2) — это квадрат со стороной 1 м или 10 дм. В квадратных метрах обозначается площадь в жилых помещениях, например: в комнатах, коридорах. Эта мерка подойдет для измерения дачного участка, спортивного зала, территории сквера.

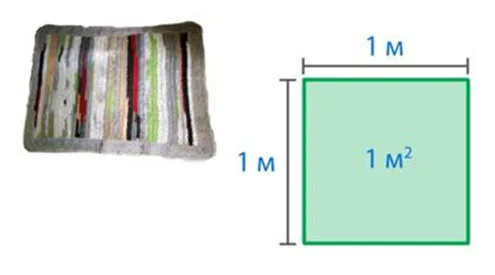
А при строительстве школ важно учитывать, сколько квадратных метров должно быть в классе, если для одного ученика по санитарным правилам нужно 4 квадратных метра. Вы хорошо справляетесь с заданиями

Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку

Вы хорошо справляетесь с заданиями. Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку.

Физкультминутка

Поднимитесь, вверх потянитесь,

Вперед наклонитесь.

Ниже, ниже тянитесь,

Достаньте мизинцем до пятки.

Получилось? Тогда все в порядке.

Выпрямитесь, грудью вздохните,

Руки шире в стороны разведите.

Соедините в замок на лопатках.

Получилось? Тогда все в порядке.

Глазки зажмурьте, спокойно постойте.

Отдохнули? Теперь посчитайте площадки.

Расчет площади фигуры по известной диагонали

Завершим статью рассмотрением вопроса вычисления площади четырехугольника, вершины прямых углов которого соединены диагональю. Рассчитаем площадь современного ЖК-монитора, если известно, что длина его диагонали с = 35 см.

Решить эту задачу можно потому, что монитор имеет стандартизированное отношение сторон, равное 16:9. Обозначая за x неизвестный коэффициент, получаем длины сторон монитора:

Теперь применяем формулу для определения диагонали, получаем:

Тогда стороны монитора и площадь его равны:

Отметим еще раз, что определить по значению диагонали площадь можно только в том случае, если известно отношение сторон прямоугольника.

Квадрат суммы

Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: \((a+b)^2\). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, \((a+b)^2=(a+b)(a+b)\). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь, и привести подобные слагаемые. Получаем:

А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:

Квадрат суммы: \((a+b)^2=a^2+2ab+b^2\)

Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.
Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.

Пример. Раскрыть скобки: \((x+5)^2\)Решение:

Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ

Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.

На всякий случай отметим, что в качестве \(a\) и \(b\) могут быть любые выражения – принцип остается тем же. Например:

Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду.

Пример. Преобразуйте выражение \((1+5x)^2-12x-1 \) в многочлен стандартного вида.

Решение:

\((1+5x)^2-12x-1= \)		Раскроем скобки, воспользовавшись формулой квадрата суммы…
\(=1+10x+25x^2-12x-1=\)		…и приведем подобные слагаемые.
\(=25x^2-2x\)		Готово.

Ответ: \(25x^2-2x\).

Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.

Пример. Вычислите значение выражения \((368)^2+2·368·132+(132)^2\) без калькулятора.

Решение:

\((368)^2+2·368·132+(132)^2=\)

               

Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего

Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: \(a^2+2ab+b^2=(a+b)^2\)

\(=(368+132)^2=\)

 

Вот теперь вычислять гораздо приятнее!

\(=(500)^2=250 000.\)

 

Готово.

Ответ: \(250 000\).

Задачи и упражнения

А теперь давайте рассмотрим несколько примеров.

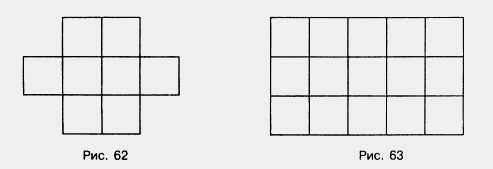
На рисунке 62 нарисована фигура, которая имеет восемь квадратов и каждая сторона этих квадратов равна одному сантиметру. Поэтому S такого квадрата будет квадратный сантиметр.

Если записать, то это будет выглядеть так:

1 см2. А S все этой фигуры, состоящей из восьми квадратов, будет равняться 8 кв.см.

Если взять какую-нибудь фигуру и разбить ее на «р» квадратов со стороной, равной одному сантиметру, то ее площадь будет равна:

Р см2.

Давайте рассмотрим прямоугольник, изображений на рисунке 63. Этот прямоугольник состоит из трех полос, а каждая такая полоска разбита на пять равных квадратов, имеющих сторону в 1 см.

Попробуем найти его площадь. И так берем пять квадратов, и умножаем на три полоски и получаем площадь равную 15 кв.см.:

Рассмотрим следующий пример. На рисунке 64 изображен прямоугольник ABCD, ломаной линией KLMN он разбит на две части. Первая его часть равна площади 12 см2, а вторая имеет площадь 9 см2.
Теперь давайте найдем площадь всего прямоугольника:

Итак, берем три и умножаем на семь и получаем 21 кв.см:

3 7 = 21 кв.см. При этом 21 = 12 + 9.

И приходим к выводу, что площадь всей нашей фигуры равна сумме площадей ее отдельных частей.

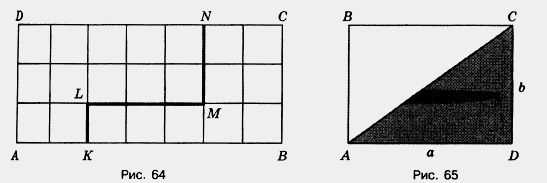
Рассмотрим еще один пример. И так на рисунке 65 изображен прямоугольник, который с помощью отрезка АС разбит на два равных треугольника ABC и ADC

А так, как нам уже известно, что квадрат – это такой же прямоугольник, только имеющий равные стороны, то площадь каждого треугольника будет равняться половине площади всего прямоугольника.

Представим, что сторона квадрата равна а, то:

S = a a = a2.

Делаем вывод, что формула площади квадрата будет иметь такой вид:

А запись a2 называется квадратом числа а.

И так, если сторона нашего квадрата равна четырем сантиметрам, то его площадь будет:

4 4, то есть 4 * 2 = 16 кв.см.

Как быть, если фигура изображена на клетчатой бумаге?

В этой ситуации нужно полагаться на количество клеточек внутри фигуры. По их числу бывает просто посчитать площадь прямоугольника. Но это можно сделать тогда, когда стороны прямоугольника совпадают с линиями клеток.

Часто имеет место такое положение прямоугольника, при котором его стороны наклонены по отношению к разлиновке бумаги. Тогда количество клеток определить сложно, поэтому расчет площади прямоугольника усложняется.

Потребуется сначала узнать площадь прямоугольника, который можно прочертить по клеточкам точно вокруг данного. Это просто: перемножить высоту и ширину. Потом вычесть из получившегося значения площади всех А их четыре. К слову, их рассчитывают как половину произведения катетов.

Итоговый результат даст значение площади данного прямоугольника.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

5 * 11 = 55

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

1. Находим количество пар в ряде натуральных чисел. В данном случае их 50.

   

   

   

   

   

   

   

   

   

   

2. Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

3. Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают

Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + ^(1/2) и P = 2b + ^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

Как найти площадь прямоугольника с разными сторонами. Площадь прямоугольника — это?

Определение. Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника.

Правило. Для вычисления площади прямоугольника, если известны длины его сторон, достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади. При необходимости результат можно укрупнить или раздробить (см. ).

Бим приложил листочек к углам донышка упаковки.

— Проверил: у упаковки четыре угла, и все они — прямые. Тогда донышко упаковки — прямоугольник.

Бом начал читать свои записи:

“Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника. Как найти площадь прямоугольника (с разными сторонами), если известны длины его сторон? Достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади”.

— Теперь надо измерить длины двух сторон. Упаковка — длинная, тогда лучше взять сантиметр.

Бим измерил упаковку.

— Короткая сторона 8 см, длинная — 72 см. Вспоминаем, что для вычисления площади прямоугольника надо длину одной стороны умножить на длину прилежащей стороны. Умножаем:

72 х 8 =576 кв.см (см2).

— Сейчас принесу из подсобки коробки, которые у меня есть, — побежал Бом.

И — надо же! — по дороге Бом встретил Олю, Колю и Васю, которые пришли пораньше на представление.

— Ребята, как хорошо, что вы здесь! Идемте, поможете нам с Бимом подобрать Буфетчице на день рождения коробку.

Бом достал из подсобки коробки, и они все вместе вернулись к Биму.

— Ребята, мы с Бимом измерили площадь упаковки конфет, которые мы хотим переложить в более красивую коробку. Красиво сложим и подарим Буфетчице на день рождения, — объяснил Бим.

— Давайте вычислим площадь донышка каждой коробки, — предложил Вася. — В коробку, у которой площадь донышка равна площади донышка упаковки, мы переложим конфеты.

— Как здорово, что Бом принес все коробки, донышки у которых имеют вид прямоугольника! — обрадовался Коля. — Как найти площадь прямоугольника с разными сторонами? Надо измерить длины двух прилежащих сторон в одинаковых единицах измерения длины и их перемножить, — получим площадь прямоугольника в единицах измерения площади. Для коробок удобнее всего измерять длины сторон в сантиметрах, а площадь самих прямоугольников уже будет в квадратных сантиметрах. Оля, давай проверим, что донышки коробок — прямоугольники.

Коля и Оля взяли листочек в клеточку и с помощью него проверили, что у донышек все углы прямые.

Затем Коля, Вася и Оля вооружились листочком в клеточку, линейкой и сантиметровой лентой и измерили в сантиметрах длины прилежащих сторон донышек коробок.

Первым управился Коля:

— У меня большая сторона 36 сантиметров и короткая 16 сантиметров. Получаем площадь моей коробки

36 х 16 = 576 (кв.см).

Следующим был Вася:

— У меня длина коробки 30 см, а ширина — 20 см. Для вычисления площади коробки надо длину умножить на ширину прямоугольника. Получаем:

30 х 20 = 600 (кв.см)

Оля измеряла тщательнее всех, ведь у нее коробка была похожа на квадрат. Но надо было убедиться, точно ли у этой коробки равны обе стороны. Так и оказалось:

— У меня прилежащие стороны одинаковые по длине, обе равны 24 см. Перемножаем длины двух прилежащих сторон, получаем: 24 х 24 = 576 (кв.см).

— Тогда у нас выходят 3 коробки с одинаковыми площадями донышек — у упаковки, — подытожил Бом:  

8 х 72 = 576 (кв.см), —

и еще у двух коробок

16 х 36 = 576 (кв.см),

24 х 24 = 576 (кв.см),

а также одна коробка  площадью больше, чем у упаковки

30 х 20 = 600 (кв.см).

— Какую же коробку выбрать? — озадаченно спросил Бим.

— Давай возьмем в виде квадрата, посмотрите какая здесь красивая крышка! — решил Бом.

Ребята выложили конфеты из упаковки в коробку.

— Ага, — посмотрел Бом. — получились три ряда. Какая же площадь донышка одного ряда? Длина ряда 24 см, ширина — 8 см. Значит площадь донышка одного ряда равна:

24 х 8 = 192 (кв.см).

Всего три одинаковых ряда

192 х 3 = 576 (кв.см).

Ура! Все совпадает!

Бим, все же, спросил:

— Сейчас мы измеряли площадь в квадратных сантиметрах. А какие еще есть единицы измерения площади?

Разность квадратов

Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:

Получили формулу:

Разность квадратов \(a^2-b^2=(a+b)(a-b)\)

Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями. 

Пример. Сократите дробь \(\frac{x^2-9}{x-3}\).

Решение:

\(\frac{x^2-9}{x-3}\)\(=\)		Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус! Попробуем воспользоваться формулой.
\(=\) \(\frac{x^2-3^2}{x-3}\)\(=\)\(\frac{(x+3)(x-3)}{x-3}\)\(=\)		Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
\(=x+3\)		Готов ответ.

Ответ: \(x+3\).

Пример.Разложите на множители \(25x^4-m^{10} t^6\). Решение:

\(25x^4-m^{10} t^6\)		Воспользуемся формулами степеней: \((a^n )^m=a^{nm}\) и \(a^n b^n=(ab)^n\).
\(=(5x^2 )^2-(m^5 t^3 )^2=\)		Ну, а теперь пользуемся формулой \(a^2-b^2=(a+b)(a-b)\), где \(a=5x^2\) и \(b=m^5 t^3\).
\(=(5x^2-m^5 t^3 )(5x^2+m^5 t^3 )\)		Готов ответ.

Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.

Пример (повышенной сложности!).Сократите дробь \(\frac{x^2-4xy-9+4y^2}{x-2y+3}\) . Решение:

Что делать, если в задаче дан периметр?

Обычно в условии указывается еще и соотношение длины и ширины. Вопрос о том, как посчитать площадь прямоугольника, в этом случае проще на конкретном примере.

Допустим, что в задаче периметр некоторого прямоугольника равен 40 см. Известно также, что его длина в полтора раза больше ширины. Необходимо узнать его площадь.

Решение задачи начинается с записи формулы периметра. Его удобнее расписать как сумму длины и ширины, каждую из которых умножить на два по отдельности. Это будет первым уравнением в системе, которую потребуется решить.

Второе связано с известным по условию соотношением сторон. Первая сторона, то есть длина, равна произведению второй (ширины) и числа 1,5. Это равенство нужно подставить в формулу для периметра.

Получится, что он равен сумме двух одночленов. Первый — произведение 2 и неизвестной ширины, второй — произведение чисел 2 и 1,5 и той же ширины. В этом уравнении всего одна неизвестная — это ширина. Нужно ее сосчитать, а потом воспользоваться вторым равенством, чтобы сосчитать длину. Останется только перемножить эти два числа, чтобы узнать площадь прямоугольника.

Расчеты дают такие величины: ширина — 8 см, длина — 12 см, а площадь — 96 см 2 . Последнее число — ответ рассмотренной задачи.